A HYBRID METHOD TO DETERMINE THE HONG KONG GEOIDProf. CHEN Yong-qi and YANG Zhan-ji, Hong Kong, ChinaKey words: geoid, GPS/leveling, gravity, integration. AbstractIntegration of all the information/data available must be performed to obtain a precise geoid. A hybrid approach of so-called sequential processing is proposed in this study, which involves two steps. The first step is to construct a gravimetric geoid using the well-developed remove-restore technique. It is then refined with GPS/leveling derived geoid heights and other information. Three methods to refine a gravimetric geoid are discussed: the least squares collocation, a multi-quadratic interpolation function, and the weighted average. The experiment with the Hong Kong geoid indicates the approach is simple and works well. 1. INTRODUCTIONDetermination of the geoid has been one of the main research areas in Geodesy for decades. More and more accurate geo-potential models (earth models) have been developed. The modern models can provide the geoid heights of any points on the earth surface with an accuracy ranging from 30 cm to a few meters (Rapp, 1997). With the development of GPS positioning technique great attention has been paid to the precise determination of local/regional geoid with an aim to replace the geometric leveling with GPS surveys. Several methods have been developed, which can be classified into two basic approaches: the geometric approach and the gravimetric approach. In a relatively small and flat area the local geoid can be determined by a combination of GPS derived heights and leveled heights, called the geometric approach. From the GPS derived heights and leveled heights at some points, the geoid heights at these points can be calculated. The geoid heights at any other points can be interpolated analytically or graphically based on these known geoid heights. A plane or low order polynomial is usually used to model the geoid (Featherstone et. al. 1998). The geometric method has been widely used in engineering projects with an area up to tens squared kilometers. The accuracy of the geoid established with the geometric approach depends on several factors, like the distribution and number of GPS/leveling stations, characteristics of the geoid in the region, and the method of interpolation. The gravimetric approach is to determine a geoid using gravity measurements. In the determination of a local and regional gravimetric geoid the remove-restore technique is widely used. However, the accuracy of gravimetric geoid is currently much below a centimeter. For instance, internal accuracy of 5.1 cm for the Belgian geoid, 6-8 cm for Latvia geoid, about 7 cm in Japan, and 5-10 cm over tens of kilometers in Canada are reported (Segawa, et. al., 1997). The factors affecting the accuracy of a local geoid using these approaches have been investigated by for instance Yang (1999), Yang and Chen (1999), Ning et al. (2000). Hong Kong has both GPS/leveling data (41 GPS/leveling stations) and 640 gravity measurements. Its local geoid has been determined by the geometric and gravimetric approaches separately (Yang and Chen, 1999; Yang and Chen, 2001). To improve the accuracy of the geoid an integration of both types of information into its determination is highly required. This paper briefly describes the two approaches as applied in the determination of Hong Kong geometric and gravimetric geoids. Then a hybrid approach is discussed with Hong Kong geoid as an example. 2. THE GEOMETRIC APPROACH AND GRAVIMETRIC APPROACHThe above-mentioned geometric approach may not give
the best accuracy. To improve the accuracy of a local geoid it was
proposed that a geo-potential model and local terrain information be
incorporated (Doerflinger, et. al., 1997; Yang and Chen,
1999). The proposed approach is similar to the remove-restore
technique used in the determination of a gravimetric geoid. Let geoid
height N be separated into three components N = NGM + NI + NT (1) where NI = N - NGM - NT (2) where NGM and NT
are the long wavelength component and terrain correction at these
stations. The values NI at these GPS/leveling
stations are then used to interpolate the corresponding values NI’
at any other points. After the predicted values NI’
are obtained, the geoid heights N’ at the predicting points
are computed by adding the long wavelength component N’ = NGM’ + NI’ + NT’ (3) This refined geometric approach was used to construct the Hong Kong geometric geoid. The information used includes: (1) the geoid heights of 31 stations derived from GPS/leveling data; (2) geo-potential model EGM96 of degree and order 360; (3) A 500m grid digital terrain model. The accuracy of the constructed geoid was checked by the GPS/leveling derived geoid heights at 6 checkpoints. The RMS of the discrepancies is 35mm. The gravimetric approach is to use gravity measurements for the computation of geoid heights. The remove-restore technique is widely used, which is well documented (e.g., Moritz, 1983). The long wavelength component derived from a geo-potential model and short wavelength component due to topographic effect are removed mathematically from the observed gravity anomalies. The Stokes’ integration of the remaining part of the gravity anomalies (called residual gravity anomaly) provides the medium wavelength component of geoid height Ndg. The final geoid heights of points are obtained by restoring the long wavelength component NGM and short wavelength component NT: N = NGM + Ndg + NT (4) The short wavelength component is the primary indirect effect on the geoid produced by the condensation of the masses above the geoid. It can be computed based on the second method of Helmert’s condensation of the topography (Wichiencharoen, 1982). The geoid heights at all grid points can be computed simultaneously with the FFT technique. The advantage of this technique is that only the data of a limited area are required for the evaluation. The authors used the above technique to construct the Hong Kong gravimetric geoid. The EGM96 geo-potential model, 640 gravity measurements and 1-km grid DTM within Hong Kong territory were used. To count for any systematic biases between the gravimetric geoid and GPS/leveling derived geoid a 3-parameter transformation was applied to the computed gravimetric geoid using the data at 31 GPS/leveling stations in the area. The results were then compared with the geoid heights at these 31 checkpoints, derived from GPS/leveling data. The RMS of the discrepancies at these points is 28 mm (Yang and Chen, 2001). 3. A HYBRID APPROACHIn the determination of the Hong Kong geometric geoid and gravimetric geoid, discussed in section 2, some kind of integration has been employed. A geo-potential model and terrain effect was incorporated into the geometric approach. In the gravimetric approach GPS/leveling derived geoid heights were used to correct the tilts and bias of the gravimetric geoid. Sometimes, this procedure is used when the accuracy of a gravimetric geoid is to be tested by comparing with the GPS/leveling derived geoid heights (e.g., Sideris, 1993). Since this procedure can improve the fitting of a gravimetric geoid with respect to GPS/leveling data, Featherstone et al., (1998) called it the combined gravimetric-geometric method. However, these attempts do not take full advantage of all the relevant information available. To further improve the accuracy of a geoid a full integration of all types of information/data must be made. There are two schemes of integration of heterogeneous data/information. One is to express different types of information/data (e.g., gravity measurements, coefficients of geo-potential model, topographical data, and GPS/leveling surveys) as function of geoid heights and solve for them. The other is here called the sequential processing. A gravimetric geoid is first constructed using gravity measurements, geo-potential model, and topographical data, and then refined using other information, such as GPS/leveling derived geoid heights. The first scheme, though rigorous, involves complicated functional models and stochastic models (weighting of different types of information). The second scheme is simpler, and its first step is a ready technique. Thus, the second scheme is used in this study. In the second scheme an important step is the integration of a gravimetric geoid and other information, mainly GPS/leveling data. The gravimetric geoid is usually given by the geoid heights at grid points. For the integration the gravimetric geoid heights at GPS/leveling stations should also be computed. The differences, denoted with dN between the GPS/leveling derived geoid heights and gravimetric geoid heights contain not only random errors in both types of geoid heights but some useful signals, these signals can be used to improve the gravimetric geoid. Note that the systematic biases of the gravimetric geoid with respect to GPS/leveling data should be removed before the integration. There are several possible methods for the second scheme of integration. One is the least square collocation (LSC). The LSC separates a difference dNi into signal and noise parts. The signals at the grid points can be predicted from all the dN values through a covariance function. The predicted signals are then added to the gravimetric geoid heights, resulting in a refined geoid. Let dN be vector of the differences at all GPS/leveling stations. The signal sp at any grid point p can be estimated from sp = cpT (C + D)-1 dN (5) where cp is a vector whose elements are the covariance of the signal at the grid point p and those at all GPS/leveling stations, C and D are covariance matrix of the signals and variance matrix of the noises, respectively, at the stations. The difficulty with the LSC lies in the selection of a covariance function. The empirical method can work, but needs large amount of GPS/leveling data to get a reliable covariance function. This method was used by Fukuda et al. (1998) for the improvement of Japan geoid. A potential problem with the LSC approach is that when the correlation distance is short or approaches zero, which may occur in many cases, the GPS/leveling data will have no contribution to the geoid determination. The second method is to use a multi-quadratic interpolation function to establish a refined geoid. The function reads
where N (x, y) is the geoid height at point (x, y),
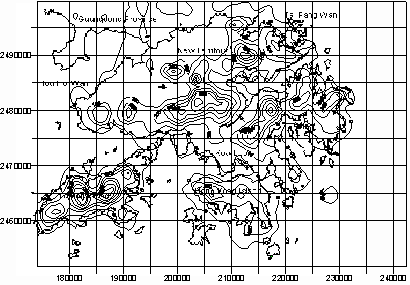
Parameter d , called smooth factor, controls the shape of the surfaces defined by the kernel function. Consideration should be given to weighting both types of information in the determination of the coefficients. The variance of GPS/leveling geoid heights is easier to estimate from their observation procedure, but more difficult for gravimetric geoid heights. It can be roughly estimated by comparing them with GPS/leveling derived quantities. Its optimal estimation can be done by using a variance-covariance component estimation technique. The third method is a simple method of the weighted average. Corrections to the gravimetric geoid heights at grid points can be interpolated using dN at the GPS/leveling stations with a weighted average method. Weight for a GPS/leveling station can be determined by Pi = 1/(Di + e)k (8) where Di is the distance between the interpolating grid point and station i, e is a constant to avoid singularity problem, and k is integer. 4. DETERMINATION OF HONG KONG GEOID WITH THE HYBRID APPROACH4.1 Data used in this studyHong Kong is a hilly territory with area about 1000 km2. There are 640 gravity measurements available with spacing 2-4 km, of which 503 observations are on land and 133 observations are in the sea. The distribution of these 640 gravity stations is shown in Figure 1. There are also 31 GPS/leveling stations, which have both GPS determined heights and leveled heights. The distribution of these stations is given in Figure 2. A DTM of 500m grid interval was created to compute the terrain correction. Figure 3 shows the topography of Hong Kong and the south part of Shenzhen. The gravimetric geoid was constructed using the technique mentioned in section 2. Refer to (Yang and Chen, 2001) for the detail. 4.2 Tests on different methodsTo test the accuracy of the geoid constructed with different methods. 6 out of 31 GPS/leveling stations are selected as checkpoints. They are points 141, 142, 139, 72, 94 and 240 (see Figure 2). Therefore only 25 GPS/leveling stations were used in the determination of the geoid. The above-mentioned three methods were used with the following details.
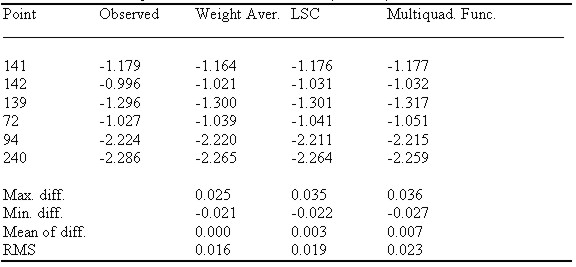
The results are listed in Table 1. It can be seen that
Table 1 A comparison of the three methods (in meter)
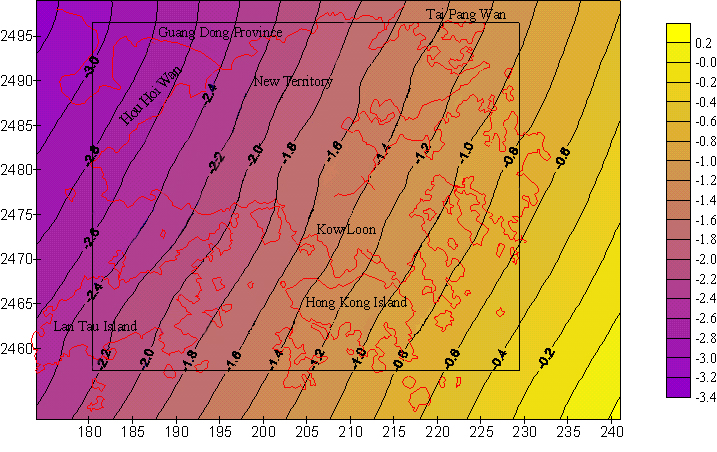
4.3 Hong Kong geoidFigure 5 shows the Hong Kong geoid, determined by the hybrid approach with the use of the weighted average method. 5. CONCLUDING REMARKSPrecise determination of a local/regional geoid is getting important, because we aim at replacing geometric leveling with GPS surveys. To this end all the information/data available should be fully utilized. There are basically two schemes of integration. One is to express all the data as functions of geoid heights and solve for them. The other is here called the sequential processing. The gravimetric geoid is first constructed using the well-developed technique and then refined by GPS/leveling data. The second scheme is not so regroups, but simpler and practical. The experiment with Hong Kong geoid indicates the scheme works well and the accuracy of the geoid is improved. The experiment also shows a simple method of weighted average can give a better result. It should be stressed that any bias and tilts of the gravimetric geoid with respect to GPS/leveling data should be removed before the integration. AcknowledgementThis project has been sponsored by The Hong Kong Research Council (project PolyU 5069/99E) ReferencesDoerflinger, E., Z. Jiang, H. Duquenne, and R. Bayer (1997). Determination of the quasi-geoid in a mountainous area: example of eastern Pyrenees (France). In "Gravity, Geoid and Marine Geodesy" (Eds. J. Segawa, H. Fujimoto, and S. Okubo), pp. 643-650, Springer. Featherstone, W.E., M.C. Dentith, and J.F. Kirby (1998). Strategies for the accurate determination of orthometric heights from GPS. Survey Review, 34, 267, pp. 278-296. Fukuda, Y., et. al., (1997). Improvement of JGEOID 93 by the geoidal heights derived from GPS/leveling surveys. In "Gravity, Geoid, and Marine Geodesy" (Eds. J. Segawa, H. Fujimoto, and S. Okubo), pp. 589-596, Springer. Moritz, H., 1983. Local geoid determination in mountainous areas. OSU Rep. No 353, Department of Geodetic Science and Surveying, The Ohio State University, Ohio, USA. Ning, J.S., Y.Q. Chen, and Z.C. Luo (2000). Strategies for the determination of a precise geoid with cm accuracy. The Proceedings of the 3rd Across-the-Strait Conference on Geomatics, Hong Kong, pp. 476-481. Rapp, R.H. (1997). Global models for the 1cm geoid – present status and near term prospects. In book: geodetic boundary value problems in view of the one centimeter geoid (eds: Sanso, F, and R. Rummel), Springer. Segawa, J., H. Fujimoto, and S. Okubo (Eds, 1997). Gravity, Geoid, and Marine Geodesy IAG Symposia, Vol. 117, Springer. Sideris, M.G. (1993). Tests of a gravimetric geoid in GPS networks. Surveying and Land Information Systems, Vol. 53, No. 2, pp.94-102. Wichiencharoen, C., (1982). The indirect effects on the computation of geoid undulation. OSU Rep. No 336, Department of Geodetic Science and Surveying, The Ohio State University, Ohio, USA. Yang and Chen (1999). Determination of local geoid with the geometric method - a case study. J. of Surveying Engineering, Vol. 125, No.3, pp.136-146. Yang, Z.J. and Y.Q. Chen (2000). Determination of Hong Kong gravimetric geoid. Survey Review, Vol. 36, No. 279, pp. 23-34. Yang, Z.J. (1999). Determination of a local geoid and its geophysical interpretation. Ph.D. thesis, the Hong Kong Polytechnic University.
Figure 1 Distribution of gravity measurements in Hong Kong
Figure 2 Distribution of the Hong Kong GPS stations
Figure 3 Topography of Hong Kong and south part of Shenzhen
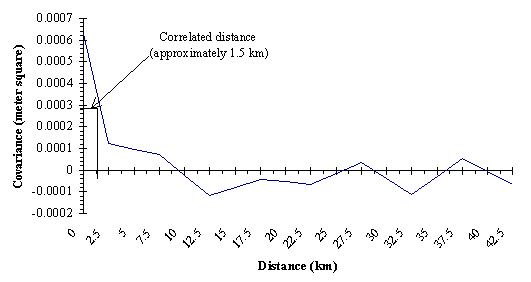
Figure 4 Covariance function
Figure 5 The Hong Kong geoid determined by the hybrid approach with the weighted average method CONTACTProf. CHEN Yong-qi, Chair and YANG Zhan-ji 9 February 2001 This page is maintained by the FIG Office. Last revised on 15-03-16. |