DYNAMIC VEHICLE POSITIONING AND ORIENTATION TECHNIQUES FOR INSPECTING ROAD SURFACE OR GUIDING CONSTRUCTION MACHINESD. STATHAS, J. KARABELAS, C. LIAPAKIS, Basil PSARIANOS and Marios KONTARATOS, GreeceKey words: Bearing diagram, GPS, Robotic total-stations, Road inspection, Paver guidance. AbstractTraditional surveying tasks (i.e. mapping of road surfaces for constructing the as-built layout) or new promising applications (i.e. paver guidance), requiring high geometric element accuracy, could well be served by dynamic positioning techniques. They can provide the basic data for constructing the bearing diagram (change of bearing along the road sections) to determine the geometric elements (i.e. the radius of horizontal curve). One technique to calculate the bearing is to use the coordinates of three consecutives points, which however are sensitive to the distance between them. Thus, their position errors degrade the bearing accuracy as well as the significant error to determine the bearing change when the vehicle moves slowly. In this paper a new technique is proposed using a GPS-based configuration with three receivers on the moving vehicle. They are installed on a moving platform forming a triangle providing the relative position of those three points with high accuracy, since they commonly "phase" most of the systematic errors of the positioning system are eliminated. As a result, the pitch, roll and lead rotations could be obtained with high accuracy as well. The method is based on the DGPS technique using RTK/OTF capability expected to provide position accuracy that could be better than 0.5cm horizontally and 1cm vertically. Experiments were conducted for assessing the configuration performance in the field and statistically testing the resulting accuracies against the theoretically expected. The experimental work has proven that determines the radius of a curved road section with the same accuracy as traditional methods. However, it appears to be very sensitive in recognizing that the machine moves within a circular path, and the most importantly in significant short distance. Additionally, this configuration provides continuously position and orientation data of high accuracy that satisfies the paver guidance operation. 1. INTRODUCTIONIn the last few years research work on automation of Road Construction and Maintenance [RCM] operations was carried out, mainly concerning excavation, pavement, pipelaying, bridge inspection, delineation and others (AHMCT 93, AHMCT 94, Drews 96, Greer 97). This research has already reached a level of maturity resulting in the development of automated machines executing individual tasks of those operations. Nevertheless, the complete discussion about automation refers to several levels: first at the tool level, second at the task level, third at the operation level, finally at the site level where several operations are executed simultaneously or in sequences (Drews 96). Seeking for solutions bottom-up the levels, increasingly the matter of integration of actions and data communication arises. This may change the way that data are collected, interchanged and viewed by the engineers during the process of monitoring, decision-making and executing those operations, or controlling the quality of work done. Possibly, even a new way of collecting, interchanging and elaborating the data at all levels could be solely a serious factor of reducing the cost of RCM operations. The basic action for proceeding to automate operations is the development of appropriate machines with sufficient intelligence, well balanced to the intelligence of a control center(s) at the field. Any level of intelligence that provides autonomy to the machine requires initially a positioning system and secondly communication for its integration to a higher level. Remaining at the machine level, its autonomy may be ensured through an architecture consisting of a positioning system, a CAD system, and robotic components. It is possible and highly recommended at the present time to develop architectures with a human operator on board. The determination of the moving machine may be achieved through remote positioning techniques and (in case of guidance) communication with the machine, or by installing active positioning systems on the machine (Psarianos et al. 98). This paper focuses on studying characteristics of an active positioning system at the machine level, located on the machine, and fulfilling the objective of collecting position data or guiding the machine. The position data determine the machine path, which could be also used for determining the constructed geometric road feature. Guidance is a complex task requiring position data, overlaying them on a CAD database, and then path correction orders [i.e. bearing corrections]. Thus, guidance systems in general include the positioning component and the trajectory interpolator, which is used for driving the machine on a given line [trajectory] (Psarianos et al. 98). Specifically, within this paper two interesting operations are discussed: The mapping of road surface and the guidance of a paver. The mapping of road surface for inspection reasons or for constructing the as-built layout necessitates a high accuracy of position data [height and horizontal coordinates]. The basic objective is to determine, possibly following a post-processing procedure, the geometric shape of the traveled trajectory. In case that the trajectory follows the road axis, then the geometric elements could be determined: radius of horizontal curve, the parameter and length of transition curve, the starting and ending points of the various features, the grades and superelevation rates. The geometry is determined by working out the entire traveled trajectory data, or possibly sections of every geometric feature constituted by points that are a-priori evaluated that belong to it. The second operation of guiding a paver necessitates the satisfaction of two objectives: the real-time determination of the machine position and orientation and the geometry of the up-to-current traveled trajectory. The latter is required in order to assess from the 'history' of the vehicle movement the deviation from the plan and thus the necessary correction of its path. This correction must be appropriately applied, so that the construction shape would be smoothly adjusted. Sudden [although accurate] changes of the path may result to gaps and to non-continuous geometric shapes. For this operation as well, a high accuracy of both horizontal and vertical shape of the road surface is required. The former bases its necessary accuracies on extensive data that well describing the geometric features, while the latter in several cases bases its calculations on a low number of data and possibly ill-suited due to fluctuations. These fluctuations could be filtered using appropriate mathematical techniques in addition to using variables based on relative positioning data rather on absolute values. While the mapping operation may be realized using just position data, the machine guidance requires further than simple position and orientation data. Furthermore, the operation speed is the significant parameter for determining the frequency of data collection. Regarding the requirements, the paving operation needs very high accuracies, probably the most demanding of all road construction and maintenance operations [Table 1].
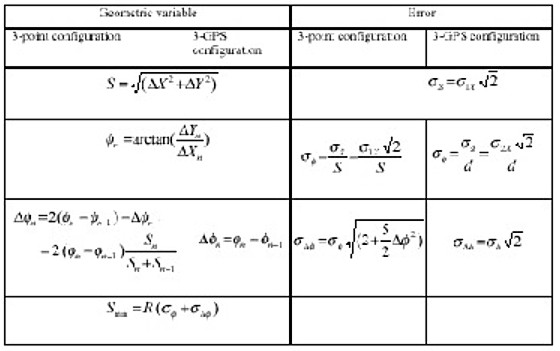
Table 1: Construction specifications of paving operation Conventional methods for staking out and for monitoring the surface geometry of the paved course are demanding, expensive and time consuming procedures. As a result, there is a need for automating the above activities using new methods, instruments and techniques (Psarianos et al. 98). 2. THE USE OF BEARING DIAGRAMThe determination of the road axis geometric elements [radius, clothoide parameter etc] as well as the determination of the location of the starting [ending] points could be carried out using positioning data. These determinations could be realized by two procedures: adjusting statistically the point coordinates to the best theoretical curve, or using the relevant bearing diagram [stationing versus bearing].
Table 2: Analysis of errors of curved trajectory The calculations based on the coordinates of consecutive points lead possibly to the determination of the geometric features, at least in case that a significant number of points are available. Contrary, the determination of the starting [or ending] point could be realized with great difficulty and relatively low accuracy. This is based on the fact that technically two consecutive road features must be smoothly adjoined, so that the drivers could easily and safely moved from one curve to the following. It is expected that the bearing diagram may alleviate this shortcoming, since the bearing change occurs in a more abrupt way. Additionally, the tangent and the curved sections are represented by straight lines, which are easily recognized from the diagram. Thus, it is easily to recognize a large number of points that belong to the specific geometric element and calculate its curvature without transferring errors from previous sections. However, the location of the starting [ending] point is subjected to the accuracy of the two adjacent geometric element calculated curvatures.
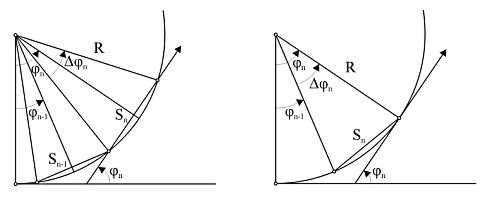
Figure 1: Bearing calculation of a) 3-point configuration, b) 3-GPS configuration The bearing could be calculated using the coordinates of three consecutive points [Figura 1a] (Klumpp 73). This bearing which in case of a curve is along the chord could be considered as parallel to the tangent applied at the middle point of the relevant arc. The exact location of this point on the trajectory requires the determination of the curve radius, which actually coincides with the determination of Δφn. Its calculation is based on three variables - φn, φn-1, Δφn-1 – which requires the use of three consecutive point coordinates. This indirect determination of the bearing leads to an accuracy depending on two types of error: the positioning accuracy of the three points and their distance S - pace of observations [Table 2]. Furthermore, the location of the arc middle point [thus the distance from the start] depends on several parameters and calculated variables. The most important are the pace and the number of points [two inversely influencing variables], as well as the errors of the bearing and the positioning. Collecting data located in very short pace, a large fluctuation of bearings may result. In this way, the calculations of geometric elements are uncertain, since the variance of these measurements is significant compared with the value itself of the bearing change. Thus, for machine guidance moving slowly measurements of points located at least a minimum distance must be used. However, this may result to a lack of the position and orientation of the machine for considerable time period fact that is unlike. The effort to deteriorate the bearing error, decreasing the positioning error and standardizing the distance between the points that calculate the bearing, was the motivation of this research. This has been achieved by performing simultaneous [synchronized] measurements of two distinctive points located on a triangle with sides of standard length. 3. A NEW CONFIGURATION (3-GPS CONFIGURATION)The new configuration consists of a triangle with three GPS receivers. In this way, all three vectors, that is pitch, roll and lead can be followed leading to bearing measurements for course and superelevation rates, while the position of the machine baseline is also continuously available. The determination of bearings may be calculated using Doppler from the code measurements, or direct measurement from the phase rate. The first way appears to be less accurate (baseline measurements with a significant noise), while the second it is not available with the commercial GPS at the present time. A third method used herein uses the coordinates of the 3-GPS points, getting in this way a mean value of two available bearings [the 3d is dependent on the other two]. To satisfy the paving operation specifications DGPS method is appropriate using Real Time Kinematic [RTK] (O' Connor 96) with On The Fly capability (Hatch 91). This technique allows the users to obtain centimeter-level up to five times per second accuracy while stationary or moving [horizontal accuracy of the order 1 - 2cm and vertical accuracy 2 - 4cm while in continuous kinematic mode]. Because these are not adequate for paving, applying a Kalman filtering [i.e. constant velocity model] the provided positioning accuracy could be improved by a factor of 3. This is especially because the dynamics of the whole procedure are extremely low [0.06 - 1km/h] and Kalman filtering acts in fact almost as a least square adjustment. Additionally, regarding cross-slope inclination etc., the relative position of GPS antennae could be obtained with much better accuracy than the absolute position in space of a single antenna, as those three antennas "phase" commonly most of the systematic errors of the GPS system. As a result, the pitch, roll and lead rotations can be obtained with much higher accuracy than the absolute positioning itself. It is expected that the differential phases would be sampled simultaneously removing in this way the variations of time biases. Actually these errors may be of several centimeters (Zimmerman and Cannon 97). After the application of the above described techniques, it was expected that the provided accuracy could be better than 0.5cm horizontally (σ2X) and 1cm vertically. Especially, when the machine moves slowly within road sections of small length (of the order of 4meters), the systematic error does not change more than 1cm for time period between 4 minutes up to 1 hour. In this case, the relevant position between the antennas would be measured with accuracy better than a few millimeters both horizontally and vertically. Obviously, the usual GPS sources of errors may confine the accuracy and the effectiveness of the system; that depend on the availability of fixes, a possible problem when there is obstruction in-between the satellite-receiver sight or other reasons [i.e. other sources of transmission]. Nevertheless, a number of benefits must also be mentioned. First, the fluctuation of pace does not influence the accuracy of the bearing and actually the accuracy of the distance from the start. Second, the very small pace does not influence heavily the determination of path characteristics. Third, although a selection of data may be realized [i.e. data every 1m in the average] for these determinations, there is a continuous position and orientation of the machine. A second configuration consisting of two robotic targets, placed on the machine, and tracked by two non-moving robotic total stations was also investigated. However, the experiment led to immature results, which are not further referred to. Initially, during the first experiments problems of synchronizations appear, which only were overcome in latter efforts. Thus, two different total stations were used with incompatible synchronization and different rates of collecting data. The outcome was that there were completely independent measurements of two arbitrary points [actually two points at the baseline of the platform by asynchronously observed], which results to a great pace fluctuation. Consequently, the results were worse than measuring with one instrument and using the 3-point configuration technique. However, this configuration would not be abandoned and searched in future time, since it has inherent advantages comparing with the 3-point method. 4. REALIZATION OF 3-GPS SYSTEMThe placement of a positioning system on a machine must comply with some basic principles such, as it must be installed (Psarianos et al. 98}:
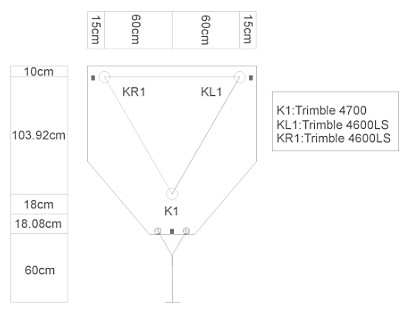
Such a place exists at the top of the paver roof. Whether the 3-GPS configuration is used, the platform must be created of three antennae forming an equilateral triangle, with a distance of 1.20m between every two antennae. This ensures a distance projected on the machine baseline - longitudinal vector length - of 1m (1.039m exactly). This platform has to be firmly connected to the "body" of the machine. Accurate measurements have to be made to connect the position and orientation of this platform with the reference points of the vehicle in order to be possible the interconnection between the external and internal orientation of the machine. By the term internal orientation, is determined the relevant position of different parts of the machine in reference to the GPS antenna.
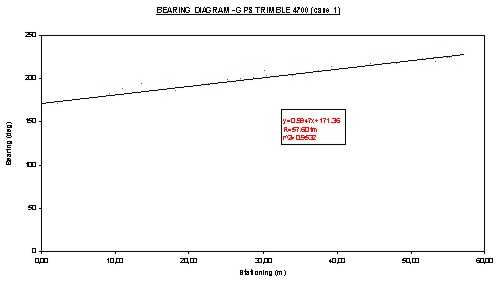
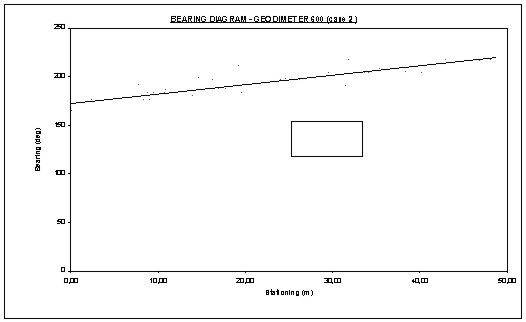
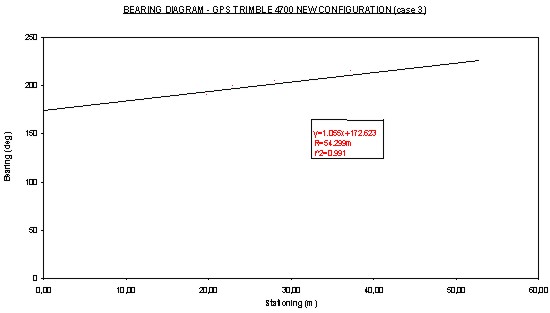
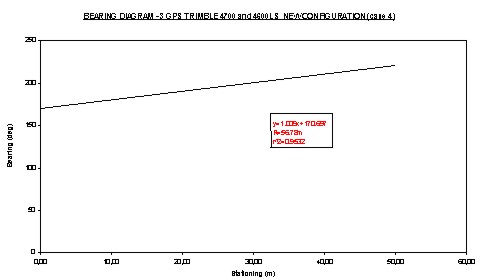
Figure 2: Platform design and image. An additional important problem concerns deviations from the desired path that the vehicle manage to follow due to slippage, difficulty to match the location and orientation of the measured points and the necessary algorithms that must be developed (Zhang and Velisky 94). It constitutes a different component of a robotic machine and therefore escapes from the interest of the present work Within the bounds of this paper, it was assumed that there exists an accurate transfer of observed position and orientation to the machine points in contact to the road surface. Thus, this work focuses on the assessment of the positioning system alone. The experiments were carried out on a target vehicle consisting of a platform traveling on three wheels from iron with no-suspension to ensure that all road anomalies would be described [Figure 2] (Katikas 2000). 5. DESIGN OF EXPERIMENTSThe objective of the experiments was to assess the effectiveness of the 3-GPS configuration and to measure its accuracy in determining the radius of a curved trajectory. The determination was made while the vehicle was considered being in the curve (φ0=0, L0=0). Thus, no assessment in the field on its accuracy in recognizing the transition from one geometric element to the next has been carried out (accuracy of the starting /ending point location). Additionally, a road section with a high curvature was selected (R=54.724m), case where rapid change of bearing occurs but in very short distances. So, while the system is expected to show a high capability to recognize bearing changes, the experiments tested the length within this could be achieved. The target vehicle was pulled on a marked trajectory of a road section consisting of a curve in several cases. These cases served various steps of the investigation. The first step regarded to the assessment of the GPS performance [autonomous system-case 1] compared with a robotic total station [target on the machine and a standing instrument - case 2]. This comparison was carried out using the 3-point traditional technique. At a second step, a sensitivity analysis was conducted to assess the influence of the pace on the radius determination accuracy [selection of points about every 1.5m and 5.0m - case 3a, 3b]. Obviously, pace fluctuation was expected due to irregular time pace observations [loss of targets, or loss of satellites etc] but also because of variations in platform speed. At a third step the 3-GPS configuration was tested [case 4], while the calculations were made elaborating all data. The coordinates of the consecutive points were almost as close as the first two cases. This was decided for experimenting initially with the worse situation but also for comparison reasons with them. Finally, a sensitivity analysis was carried out in order to determine the radius from the first 10% and the 25% of the points [cases 5a,5b]. In this way, the accuracy of the system may be assessed while the radius must be calculated from up-to-current traveled trajectory. The instruments used are the following.
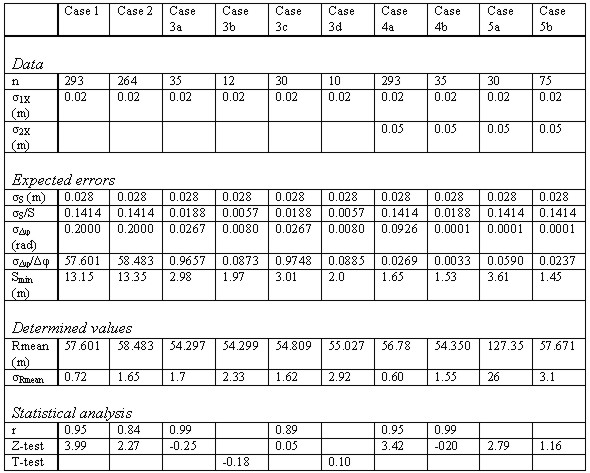
The expected accuracy of coordinate determination was 2cm [σ1X = 2cm]. This value has been revealed from an extensive experimental work carried out by the authors with robotic total stations (Stathas and Karabelas 2001). The Geodimeter 600 could realize a point measurement within 0.4-0.7sec with an accuracy of ±6mm±2ppm. A similar accuracy is expected by the GPS using RTK/OTF capability 6. RESULTSThe analysis initially aims at assessing the calculated radius values by compared them with the known one. Secondly, its capability of the various cases to recognize that the platform moves within a curve is evaluated. Finally, its sensitivity of the path deviation is tested. The first assessment was carried out by using statistical test, since the R-values of the various samples are assumed to be normally-distributed around the known value (for small samples the t-test was used). The second assessment was based on the determination of the correlation coefficient of the regression line of the bearing diagrams. The third assessment was based on estimating the minimum distance required to determine an appropriate bearing change that is greater than the expected errors (Smin = R (σφ + σΔφ). All calculations are stated in Table 3, and the results may be interpreted as follows. First, the estimation of the radius using the 3-point configuration does not vary using a DGPS technique or a robotic total station [cases 1&2]. In both cases, the deviation of the radius value from its exact value may be sought to the very small pace (dense observations) that strongly affect the bearing fluctuation. However, the correlation coefficients for using data from the entire path are high which shows that even a strong cloud of data is capable to indicate that the platform moves within a circular section.
Table 3: Expected errors and statistical analysis (5% level of significance: Z=1.96, T=2.20 and n-1=11, T=2.26 and n-1=9) Second, increasing the pace using both DGPS and a robotic total station positioning techniques indicates that in general a significant improvement of the radius value and its accuracy may be achieved [cases 3a,3b,3c,3d]. However, for small curves (60m length) the increase of the pace leads to relevant decrease of the number of points, which results to possible small samples. Obviously, there should be a value of pace than further the accuracy may be degraded, which is expected to be greater than 5.0m. Additionally, it must be mentioned that all calculations were based on the fact that the chord approach satisfactorily the arc [Table 1]. For large chords (say around 15.0m) this does not hold and a further correction should be made which complicates the error analysis calculations.
Figure 4: Bearing diagram including all data mean pace: 0.20m Third, although the pace was hold to a very small magnitude, the 3-GPS configuration shows a considerable improvement in calculating the radius [case 4a]. However, in the field this improvement was not fully proven, since the radius value was accepted to represent the real value by its accuracy is hold low. Contrary, the regression coefficient shows an excellent correlation, which indicates the high capability of the method to recognize the circular path. This results to accurate estimation of the stationing of various points (when the radius is known from the CAD), and further an accurate estimation of the ending point of the curve. Additionally, the sensitivity of recognizing a path deviation is high (Smin=1.6m), and most important being independent of the mean pace of observations.
Figure 5: Bearing diagram with one GPS on the platform - case 3a [mean pace 1.5m] A radical improvement was realized when the 3-GPS method was used with a pace approximately of 1.5m [case 4b]. It appears that in terms of radius calculation this case does not varies from the case 3a. Finally, a low percentage of data representing the case of 'up-to-current traveled trajectory' derives problematic values for radius [case 5a,5b]. This means that although the new method provides good estimates for path deviations could not within the first parts of the curve determine the traveled trajectory. This means that a real time repathing strategy could not be defined accurately. However, this is possible after the first 25% part of the curve.
Figure 6: Bearing diagram including all data mean pace: 0.20m- case4a [3-GPS configuration] This research provides evidence that the proposed configuration has the potential to calculate the radius of a curve, however, with similar accuracies with the traditional methods. Still the adequate large pace seems to dominate the determination accuracy. Nevertheless, the 3-GPS configuration recognizes very early the circular trajectory of the road. This leads to successful recognition of the starting point of the curve. Additionally, a considerable benefit for machine guidance and operation is the provision of bearing and positioning at any time with higher accuracy. 7. FURTHER RESEARCHThe 3-GPS configuration seems promising, however, more experimental work must be carried out to establish its capability. Investigations must be conducted for transition sections (clothoide or recognition of starting /ending points), where the control on the errors of every individual observation is more important than of a least-squared adjusted variable resulting from a large number of points. Furthermore, a sensitivity analysis must be performed for cases with sections of small length (usually low categories of roads with continuous varying and high curvature), and sections with very large length but low curvature (high categories of roads). In both cases the machine guidance task is more concerned about the positioning and orientation accuracy of the machine rather to describe the exact path traveled within small time paces. Finally, the grade and superelevation rate determination must be tested, since height determination is very demanding for paver operation. 8. CONCLUSIONSThe proposed autonomous system provides continuous position and orientation data, very important function for paver operation and surface material placement. It shows a significant capability in recognizing the circular path of motion, which leads to accurate determination of stationing of all points in the curve. Finally, it seems to be more sensitive to recognizing path deviations. Contrary, it was not proven as more capable to determine the radius value, which still remains a matter of the pace of observations and most important its fluctuation. Thus, the proposed configuration appears to indicate superiority over other tools for machine guidance but not for inspecting or mapping the as-built road sections. REFERENCESAHMCT (1993): Aerial Bridge Inspection,UC Davis. http://www-ahmct.engr.ucdavis.edu/ahmct/AHMCT_projects/aerial.html AHMCT 1994): Automated machine for cone placement and retrival, UC Davis http://www-ahmct.engr.ucdavis.edu/ahmct/AHMCT_projects/cone.html Drews P. (1996): Operator Assisted Mobile Road Robot for Heavy Duty Civil Engineering Applications, ESPRIT Project 6600, Final Report, APS GmbH, Aachen, Germany. Greer R., Y-S Kim and C. T. Haas (1997): Telerobotic Control for Automated Pavement Crack and Sealing, Transportation Research Board 76th Annual Meeting, Jan. 12-16 1997, Washington D.C. Hatch R (1991): Ambiquity Resolution while Moving Experimental Results, In Proceedings of the 4th International Technical Meeting of the Satellite Division of the ION, GPS-91, Albuquerqe, Sept. 1991. Katikas M. (2000): Investigation of Geometric Elements Determination of Roads using Dynamic Positioning and Orientation Systems, Master's Thesis, National University of Athens, Athens, Greece (in Greek). Klumpp R. (1973): Achsberechnungen mit Hilfe der Ausgleichungs- und Optimierungsrechnung, Dissertation, Deutsche Geodätische Komission,, München, Beck'schen Verlag. O'Connor M., G. Elkaim. And B. Parkinson (1996): Carrier Phase DGPS for Closed Control of Farm and Construction Vehicles, Journal of Institute of Navigation, Volume 43, no. 2. Psarianos B. and M. Kontaratos (1998): Automated and Robotic-based Techniques: New solutions for road construction and maintenance, Final Report, Project RO-97-SC1007, DGVII, EE, National University of Athens, Athens, Greece. Seward D. and F. Margrave (1996): LUCIE the Robot Excavator - Design for System Automation, April 1996, pp. 963-968, Minneapolis, Minnesota USA. Stathas D. and J. Karabelas (2001): The use of a Robotic Total Station in Testing the Trajectory of a Moving Target, Geomatics Research Australasia, The Institution of Surveyors, Australia Inc. (to be published). Zhang Y. and S. Velisky (1994): Tracking Control Algorithms for the Tethered Mobile Robot, Interim Report, AHMCT, UC Davis, June 1994. http://www-ahmct.engr.ucdavis.edu/ahmct/AHMCT_projects/tether.html Zimmerman K.R. and R. H. Cannon Jr. (1997): Experimental Demonstration of an Indoor GPS-Based Sensing System for Robotic Applications, Journal of Institute of Navigation, Volume 43, no. 4. CONTACTD. Stathas, J. Karabelas and B. Psarianos C. Liapakis Marios Kontaratos 20 April 2001 This page is maintained by the FIG Office. Last revised on 15-03-16. |