Application to Leveling using Total StationJongchool LEE and Taeho RHO, KoreaKey words: Total station, Indirect leveling method, Incidence angle, Regression analysis. AbstractTotal Station are spread to many measuring sites, however, their functions are not fully understood yet. Leveling is one of the misunderstandings. The indirect leveling method using total station for leveling is considered to have due accuracy, applications of the indirect leveling is gradually expanding for public works such as construction of roads, airports and cities. Instead of direct leveling method, indirect leveling method using total station is applied in this research to assure the technicians in performing the tests, it is more economical as well. The results are expected to be used for many public works including routine survey, wide residential land development and subsidence measuring instruments. 1. INTRODUCTIONAt present, Total Station has been widely spread and used in many survey sites, and sometimes it is not fully used since users misunderstand the principles of this unit. One of them is the leveling, and in case we use Total Station for leveling, this is classified as the indirect leveling method, and since it is judged that this method can maintain the considerable accuracy, now it has been increasingly used for many public works such as road, airport and city etc. This study empirically made a research in the improvement of accuracy of precise leveling by using the indirect leveling method, Total Station that can more simply and quickly find elevation by replacing the direct leveling. 2. MEASUREMENT PRINCIPLE & ERROR OF EDMThe principle of the measurement device, EDM, which is currently used, is that it calculates the distance by measuring the phase shift during the radiated light wave from EDM's main unit returns by being reflected through the reflector, which is positioned at measurement point. This phase shift can be regarded as a part of frequency that appears as the unit of time or length under a specific condition.
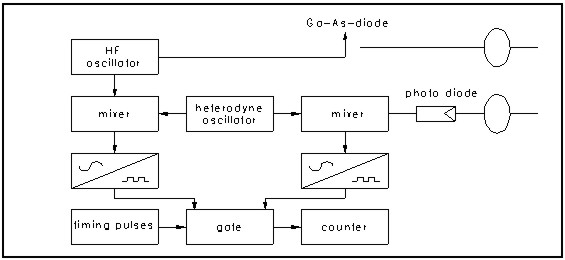
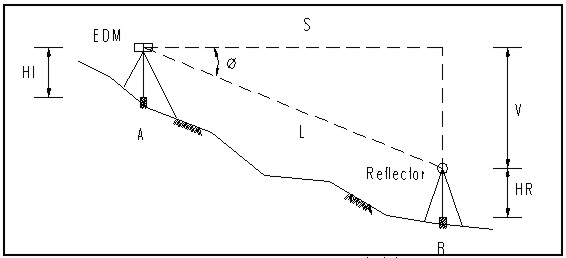
Figure 1. EDM's structure When the slope distance L and slope angle Elevation of Point B = Elevation of Point A + HI±L
sin
Figure 2. EDM's measurement principle 2.2. EDM's errorThe distance measured by EDM is expressed as the formula (2-2).
Here, we have
If we measure repeatedly 2 or 3 respectively different
wavelengths in order to check Value
Though electronic wave's velocity
Here, we have We should measure the temperature and humidity in the
air according to measurement line if we try to find the exact Value If we substitute formula (2-4) for formula (2-3), the
Value
and if we assume the wavelength under a specific
atmosphere condition is
we can express EDM's distance If it is
and at this time, the real distance
From the formula (2-7) and formula (2-8), we can get
and the corrected distance, that is, the correction formula of the measurement distance under a specific atmosphere condition is expressed as the following formula (2-10).
In order to find the final corrected distance, we
should correct the error of EDM's zero point
Here, we have
If we substitute the formula (2-6) and (2-10) for
(2-11), the corrected distance is as follows.
The variance of the distance
And if we simply express the formula (2-13) by
Here, we have EDM's accuracy is expressed as the following general formula.
And if we express the formula (2-14) by the form of
formula (2-15),
Here, we have
3. EDM'S ERROR CORRECTIONThe device for measuring distance by light wave always should have the correction for the measured value. Every kind of distance measurement device is the same, but they are generally influenced by the following factors. Since the weather condition already exists, the difference of influence made by measurement devices is combined with the observation variable that we can directly observe and the non-observation variable that we can not directly observe. The variables that are possible to observe and
determine a specific condition are temperature, atmospheric pressure
and steam pressure, and the effect of them is various. The refraction
index is calculated by the variables of temperature, atmospheric
pressure and steam pressure, and it determines the ratio between the
velocities of electromagnetic wave's electric wave under vacuum ( Though the measurement signal progresses the same distance with the various velocities according to the weather condition, since the computer installed at the measurement device is programmed in advance to use a certain fixed wave velocity, this velocity deviation comes to generate the signals in proportion to the measured distance.
Here, we have
The variables that are impossible to directly observe and influence on the measurement process are rapid weather change, rainfall, heat haze and fog etc. Therefore it is desirable necessarily to correct the factors that largely influence on the measurement result, as much as possible. The variables to be corrected are refraction of atmosphere, height of sea level, refraction by projection method and difference of scale coefficient and so on.
Here, we have
The distance correction value,
Here, we have
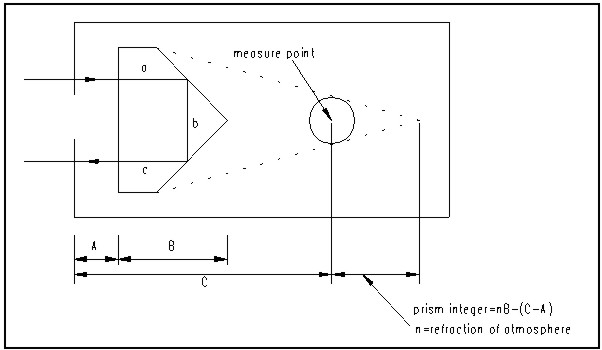
3.2. Zero correction3.2.1. Installation of reflector Since a prism reflector decreases if its slope angle is getting bigger to prism face, and it has much dispersion of light if measurement distance is getting longer, we should install a reflector uprightly facing to a measurement device when we install it. (1) Prism integer: The light radiated from the distance measurement device by light wave is reflected through the inside of prism, and if we convert the inside length into the distance in the air, it becomes longer two times. It is shown in Fig. 3 as follows.
Since a prism has its own integer, it is better to use
a prism that exactly fits to a distance measurement device by light
wave, and if we use it under the condition that a prism's integer is
wrong or it is not exactly adjusted, we may get large measurement
error. In Fig. 3, the distance we actually measure is Line Since the refraction index of prism is higher than the
atmosphere, we should consider this refraction index and decide it,
and generally the prism's integer
Here, we have
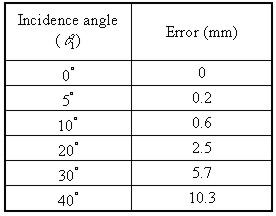
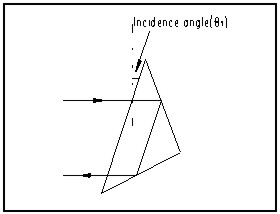
Figure 3 Prism integer (2) Error by incidence angle Since the error happens according to the light angle that enters into a prism, it is desirable to set up a prism side vertically and exactly to the measuring point when we set up a prism. The following Table 1 shows the experimental value that TOPCON Co. executed at 1km section by prism's incidence angle. Table 1 Distance error volume by
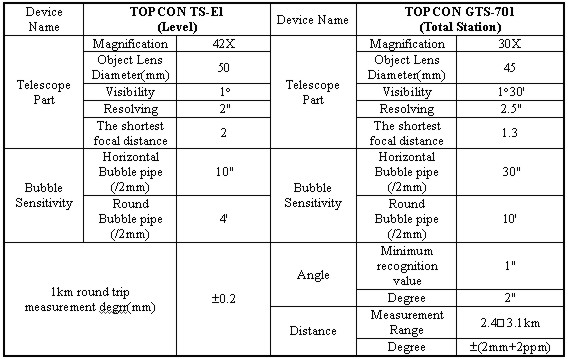
Figure 4. Distance error by Incidence angle 4. MEASUREMENTWe selected the asphalt-paved road equivalent to total 650m near Namchun-Dong, Sooyoung-Ku, Pusan, Korea as the measurement object area. We used TOPCON's GTS-701, Total Station as the measurement device, and in order for us to compare the accuracy, we also used TOPCON's first class leveling device as the leveling device, and the specifications for each device is as shown in the following Table 2 Table 2 measurement device
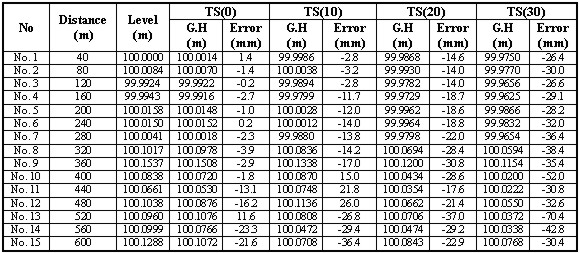
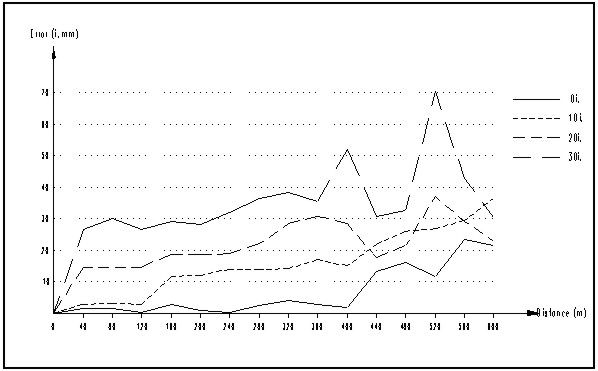
4.2. Measurement MethodWe selected a random point (No. 0) in the measurement object area, and we set out total 15 measuring points at the same 40m intervals from that point as reference. The distance between a target staff and a device is decided by several conditions, and since the collimation distance of leveling that requires high precision is 40m, this study also set the same interval of the target staff as 40m and measured each measuring point by the first class leveling device. And when we measured it by Total Station, we fixed the device at the reference point(No. 0), and made the heights of the device and reflector same, and we selected the direction of the incidence angle that faced downward, and we measured and compared it with the value that was measured by the first class leveling device and analyzed it. 4.3. Measurement result and analysisThe result that we measured respectively three times by the first class leveling device and Total Station and calculated the average value is as shown in Table 3 and Fig. 5. As a measurement result, it showed that the rearranged error to the distance of 600m measured by the first class leveling device was 0.6mm, and it satisfied the allowable error of the first class leveling, 1.9mm. And in case measuring by Total Station, it showed that the maximum distance to discriminate was 280m, and if we see the measured value without a prism's incidence angle, the error was 0.2∼23.3mm. These are the values appeared by each distance for No. 0 point, and it is considered that they appeared because of the observer's collimation error, light wave's dispersion coming from Total Station's main unit and since it was not vertically positioned to the exact central point of a prism. And when measuring by Total Station, we could calculate the correlation between the incidence angle and the error volume as the form of Table 3 Measurement result
Figure 5 Measurement result 5. CONCLUSIONAs a result that we measured the indirect leveling by Total Station, it was observed that the maximum distance we could discriminate the prism's central point from the telescope lens was 280m, and its error was 2.3mm that satisfies the second class allowable error, 2.6mm. Therefore it is judged that if we apply the distance that can discriminate the prism's central point, it can satisfy the second class leveling. From the result that we made the regression analysis
on the correlation of prism's incidence angle when measuring an
indirect leveling by Total Station, the following correlation was
formed at the distance of 0∼400m.
REFERENCES
CONTACTProf. Jongchool Lee Taeho Rho 20 April 2001 This page is maintained by the FIG Office. Last revised on 15-03-16. |