Within the last decade, GNSS Precise Point Positioning (PPP) has
generated unprecedented interest amongst the GNSS community and is being
used for a number of scientific and commercial applications today.
Similar to the conventional relative positioning technique, PPP could
provide positioning solutions at centimeter-level precision by making
use of the precise carrier phase measurements and high accuracy
satellite orbits and clock corrections provided by, for example, the
International GNSS Service (IGS). The PPP technique is attractive as it
is computationally efficient; it eliminates the need for simultaneous
observations at both the reference and rover receivers; it also
eliminates the needs for the rover receiver to operate within the
vicinity of the reference receiver; and it provides homogenous
positioning quality within a consistent global frame anywhere in the
world with a single GNSS receiver. Although PPP has definite advantages
for many applications, its merits and widespread adoption are
significantly limited by the long convergence time, which restricts the
use of the PPP technique for many real-time GNSS applications. We
provide an overview of the current performance of PPP as well as attempt
to address some of the common misconceptions of this positioning
technique – considered by many as the future of satellite positioning
and navigation. Given the upcoming modernization and deployment of GNSS
satellites over the next few years, it would be appropriate to address
the potential impacts of these signals and constellations on the future
prospect of PPP.
INTRODUCTION
In recent years the Global Navigation Satellite Systems (GNSS)
Precise Point Positioning (PPP) technique has increasingly gained
interest and widespread adoption within the GNSS community. A number of
governmental, academic and commercial PPP services have been established
to support scientific and commercial Position, Navigation and Timing
(PNT) applications. In March 2012, the first international symposium on
PPP organized by the German Federal Agency for Cartography and Geodesy
(BKG) was held in Frankfurt am Main, Germany. The symposium brought
together experts from universities, governments and the private sector
to discuss technical issues relating to PPP. It was a great success,
with 180 participants from more than 30 countries. In the following year
in June 2013, the International Association of Geodesy (IAG) in
partnership with NRCan, the International GNSS Service (IGS) and York
University hosted a second international PPP workshop in Ottawa, Canada.
Such workshop activity is indicative of the prominence given to PPP as a
powerful PNT technique for next generation satellite navigation.
For three decades, relative (or differential) positioning has been
the dominant precise positioning and data processing technique. In
relative positioning, the coordinates of a point are determined relative
to another reference point with known coordinates. This eliminates or
reduces most GNSS observation errors that are spatially correlated at
both the unknown and reference points, thus providing high accuracy
positioning solutions. Originally, the implementation of this relative
positioning technique for many commercial applications involved one
reference station and one or more rover receivers operating in a local
area, in real-time. Centimeter- to submeter-level positioning accuracy
can be obtained, with the accuracy mainly dependent on whether the
pseudorange or/and carrier phase observations are used, and in the case
of the latter, whether ambiguity resolution was successful. Carrier
phase processing provides the most accurate positioning results, in
real-time and in dynamic mode, in a technique known as “Real-Time
Kinematic” (RTK). RTK is now, and has been for many years, the industry
standard procedure for precise positioning and navigation applications
such as machine control, precision farming, surveying, and mapping
(Rizos et al. 2012). But this technique was soon augmented to a regional
network of reference stations that permitted the extension of the
service coverage area in the so-called “network-RTK” mode.
PPP emerged as an alternate GNSS positioning technique in the late
1990s (Zumberge et al. 1997). PPP in the standard mode utilizes
dual-frequency pseudorange and carrier phase observations from single
GNSS rover receivers, and requires precise satellite orbits, clock
corrections (and other error modeling) to generate high accuracy
positioning solutions. The PPP and relative positioning approaches were
originally established independently of each other, to address different
purposes. PPP was first developed to enable efficient processing of
large global networks of GNSS data. It quickly emerged that it is also a
viable alternative to the traditional relative positioning technique
because it does not have the limitations of the latter, such as the need
for a nearby reference station and the associated baseline length
constrain. One major drawback of PPP, however, is the long solution
“convergence time”. It can range from tens of minutes to several hours
(Bisnath and Gao 2009; Hèroux et al. 2004; Kouba 2009).
The motivation for this paper is to extend the work of Bisnath and
Gao (2009) and Rizos et al. (2012) who described the performance of PPP
technique and speculated on its future potential. The goal is to provide
an insight into the current prospects of PPP and to address some of the
common misconceptions concerning this positioning technique such as the
current performance of PPP; PPP Ambiguity Resolution (PPP-AR) and
validation; the use of ancillary data such as atmospheric information
derived from regional reference stations networks to aid integer
ambiguity resolution and re-convergence; the importance of PPP
“infrastructure” that allow precise orbits and satellite clocks to be
determined; as well as the data dissemination mechanisms which are
mandatory for real-time PPP. Given the upcoming modernization of GPS
signals and the deployment of other GNSS and Regional Navigation
Satellite Systems (RNSS) satellites, it is necessary to speculate on the
potential benefits and challenges of these additional signals and
constellations in the context of multi-GNSS PPP.
COMMON MISCONCEPTIONS IN PPP
This section addresses some of the common misconceptions in PPP,
e.g., how good a PPP solution is and if phase ambiguity resolution in
PPP could speed up the long convergence time. It will also elucidate
possible technical limitations and prospects of using PPP technique in
real-time PNT applications.
How Good is a Standard-PPP Solution?
The metrics used to assess the quality of the PPP estimates are:
accuracy, precision and convergence time. In PPP there is minimal
difference between accuracy and precision as the residual biases are
typically at centimeter level owing to the rigorous error modeling in
PPP. The convergence time is defined as the time required for the
position or ambiguity estimates to reach a specific level of accuracy,
and do not deviate beyond this level after reaching it. In practice,
each user often uniquely defines the level of accuracy for convergence.
Numerous researches have shown millimeter- to centimeter-level point
positioning accuracy can be achieved for static dual-frequency PPP
processing using a 24-hour good quality dataset (Colombo et al. 2004;
Gao and Shen 2002; Hèroux and Kouba 2001; Kouba 2009; Witchayangkoon
2000; Zumberge et al. 2001). Seepersad and Bisnath (2014) investigated
the performance of the standard-PPP technique in static and kinematic
mode using one week datasets collected from 300 IGS stations from 1-7
July 2012. Dual-frequency ionosphere-free combination of GPS
measurements was used together with the IGS 5-minute final orbits and
30-second clock correction information. The tropospheric delay was
estimated as part of the adjustment process and no integer PPP ambiguity
resolution was attempted in their investigation. The IGS accumulated
weekly SINEX station coordinates were used as reference. They concluded
that PPP in static mode could provide positional accuracy of 7 and 13 mm
in the horizontal and vertical components, respectively using such a
24-hour dataset. In kinematic mode, the conservative accuracy of the
horizontal positioning component was 46 mm, and 72 mm in the vertical
component. It is expected that the estimated vertical component will be
less accurate than the horizontal component due to the satellite
geometry as well as the quality of the correction models used, e.g.,
tropospheric modeling for estimating the tropospheric delay. It was also
shown in Seepersad and Bisnath (2014) that the quality of estimated PPP
solutions is linked to the geographical location of the stations. Some
stations portrayed less accurate position estimates and longer
convergence time, which may be attributed to the weak estimation of the
wet component of the tropospheric delay, as well as modeling of other
PPP related errors such as solid Earth tides and ocean loading.
The PPP solutions in static mode were slow to converge, with
approximately 20 minutes required for 95% of solutions to reach a
horizontal accuracy of 20 cm or better; and the convergence time was
much longer for kinematic processing (Seepersad and Bisnath 2014). As a
general rule, a minimum of one hour is required for the horizontal
solution from a standard-PPP static processing to converge to 5 cm.
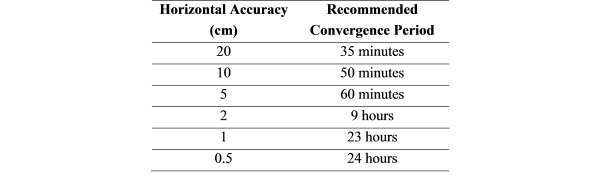
Table 1 lists the recommended convergence time for static PPP to achieve
the required horizontal accuracy. It should also be noted that the
quality of the position estimates is very dependent on the observation
session length, the geographical location of the receiver, the number
and geometry of the visible satellites, user environment (i.e. the
degree of multipath disturbance), and the quality of the observations.
Table 1 Recommended convergence time for static PPP solution to
converge (Seepersad and Bisnath 2013).
PPP Ambiguity Resolution
Standard-PPP with “float ambiguities” is an adequate technique for
long period static applications, but certainly not for short observation
sessions and/or kinematic operations. In standard-PPP the carrier phase
ambiguity is a combination of the integer ambiguity term and hardware
dependent biases originating from the satellites and receivers, thus
resulting in the phase ambiguity term being a real-valued quantity. This
is true for any single receiver positioning using carrier phase
measurements, which explains why PPP requires an extended convergence
period to reliably estimate these “float ambiguities”. In contrast, in
relative positioning the double-differenced ambiguity term, between two
receivers and two satellites, has an integer nature (hardware dependent
biases have cancelled) and consequently can be “fixed” to the correct
integer value, thus enabling instantaneous positioning in real-time.
Since 2007, a number of researchers have been making progress on the
challenge of resolving carrier phase ambiguities in PPP processing. In
general, there are two methods: the “Uncalibrated Hardware Delays”
method (Bertiger et al. 2010; Ge et al. 2007); and the
“Integer-Recovery-Clocks” (Laurichesse et al. 2009) or “Decoupled Clock
Model” (Collins 2008) method. An in-depth discussion can be found in
Geng et al. (2010) and Shi (2012). It has been shown that the
ambiguity-fixed position estimates from these methods are theoretically
equivalent (Geng 2010; Shi 2012). The term “fixed-PPP approach” is used
here to describe PPP processing with phase ambiguities resolved. The
benefit of correct integer ambiguity fixing is that it can shorten the
convergence time thus potentially improving the accuracy and consistency
of PPP solutions.
Implementation of the fixed-PPP approach requires that modeling and
processing be standardized at both the service provider and user-end
(Teunissen and Khodabandeh 2015). The above-mentioned PPP-AR methods
vary in terms of the strategies used to separate the hardware delays
from integer ambiguities. Therefore, fixed-PPP is only possible provided
the service providers also deliver to users estimates of the hardware
biases, in addition to the satellite orbits and clocks, which are
consistent and suited for PPP ambiguity fixing.
Figure 1 shows the average rate of convergence of float-PPP and
fixed-PPP positioning as a function of horizontal and vertical position
errors. Similar to the processing strategy adopted by Seepersad and
Bisnath (2014), the dataset used was one week of data from 1-7 July 2012
from approximately 300 globally distributed IGS sites. Only GPS data
were processed in static mode and the IGS accumulated weekly SINEX
station coordinates were used as reference. In this instance, both
float- and fixed-PPP solutions were computed. It can be seen that
ambiguity fixing provides an improvement in the horizontal component
estimates, and to a lesser extent the vertical component. There is
generally little difference between the float and fixed solutions during
the first 15 minutes of the solutions and after 6 hours. In fact, it is
interesting to note that during the first 15 minutes the float solution
is slightly better than the fixed solution, i.e. a specific time period
is still required for the float solution to converge to ensure correct
integer fixing.
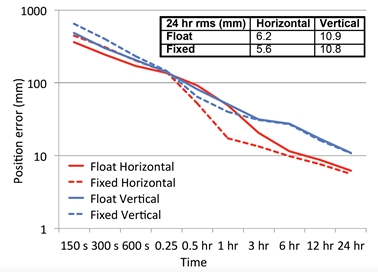
Fig. 1 Average position error of float-PPP and fixed-PPP solutions.
The carrier phase ambiguity is a unique random constant for each
continuously tracked station-satellite arc. The only direct source of
information on its value is from each corresponding pseudorange
observation. This means that the ability to derive as estimate of the
ambiguity is strongly influenced by the quality of the pseudorange
observations, and to a lesser extent the carrier phase observations. In
PPP, the convergence period occurs as the solution transitions from a
pseudorange-only solution to a float-ambiguity carrier phase solution.
The pseudorange observations are filtered by the smoothly varying
carrier phase observations, which leads to a convergence period after
the initialization of the solution. This highlights the fundamental
paradox of PPP-AR in that a substantial convergence period is still
required.
Furthermore, the PPP-AR technique may not necessarily be able to
consistently resolve the ambiguities correctly, or to maintain fixed
solutions throughout the processing given the inherently weaker model of
PPP (Bisnath and Collins 2012). This could significantly degrade the
quality of the estimated position solution. Some standard ambiguity
search and validation methods, e.g. the ratio test and their empirical
thresholds, do not work well for PPP-AR, especially when the satellite
geometry is poor (Collins et al. 2009; Shi 2012). Therefore, rigorous
integer ambiguity validation methods specifically applicable for PPP
remain an issue to be investigated.
Is PPP Ambiguity Resolution a Solution to All Problems?
Isolating the phase ambiguities as integer values in PPP does not by
itself permit rapid ambiguity resolution (Collins and Bisnath 2011). The
convergence period of standard float-PPP processing remains, which
constrains the adoption of the PPP technique for real-time GNSS
positioning and navigation applications. What is even more problematic
is that this convergence process has to be repeatedly applied whenever
satellite tracking loss occurs, which further devalues the
practicability of real-time PPP. So the problem of convergence for
fixed-PPP is not only an issue after a receiver’s cold start but also
after any interruption of the measurement due to signal obstruction.
The key to instantaneous AR for short baseline RTK lies in the a-priori
knowledge of the ionosphere. In short baseline RTK, the ionospheric
delay is almost completely corrected for using the nearby reference
station observations. This significantly enhances the underlying model
strength making rapid ambiguity fixing possible (Teunissen 1997). The
implication for PPP is that the elimination of the ionospheric delay on
measurements using traditional linear combinations is not adequate to
facilitate rapid AR. In fact, the convergence period for PPP will not be
changed significantly by simply because the ambiguities are
integer-valued as seen in previous section.
It has been shown that explicitly estimating and constraining the
ionosphere within the PPP-AR model can permit instantaneous
“re-convergence” of PPP solutions after cycle slips have occurred
(Banville and Langley 2009; Collins and Bisnath 2011; Geng et al. 2010;
Zhang and Li 2012). When signal lock to a satellite is lost, the
ionospheric delay estimates are extrapolated from previous epochs in
order to “constrain” the ionosphere until the GNSS signal is
re-acquired. This method can be used globally and is effectively
independent of any local or regional network. However, the efficiency of
this method is somewhat limited and is not suitable, for example, when
cycle slips occur during large ionospheric fluctuations or the
observation dataset has long data gaps.
The second approach, which specifically deals with instantaneous
ambiguity fixing after a receiver cold start, is to incorporate
externally-derived ionospheric information (Juan et al. 2012). In
principle this information can be obtained from ionospheric models such
as the Klobuchar model or the Global Ionospheric Maps (GIMs), which may
result in some improvement in ambiguity fixing. However, it still
requires a considerable time (more than 10 minutes) to fix the initial
phase ambiguities to integer values. This is because GIMs with a nominal
accuracy of 2-8 TECU in the vertical (not slant) direction are not
sufficiently accurate to serve as a robust constraint for rapid
ambiguity fixing (1 TECU corresponds to 16.3 cm range error). Figure 2
shows the errors of single-differenced ionospheric delays on GPS L1 at
MOBS IGS station calculated using post-processed GIMs provided by the
IGS on 13 August 2014. The L1 ionospheric delay errors varied between 47
cm and 69 cm RMS, which corresponds to 2-3 TECU of slant TEC (Total
Electron Content) errors. The accuracy with which the ionospheric
corrections need to be provided depends on the wavelength of the GNSS
signals used. Therefore the required accuracy of the ionospheric
corrections must be better than a few centimetres to allow
rapid-to-instantaneous ambiguity resolution in PPP. Another possible
solution is to use externally-derived ionospheric delay estimates from a
dense regional GNSS reference network (Li et al. 2010). This approach
makes possible instantaneous ambiguity fixing within seconds, which is
equivalent to RTK performance. However, this approach is only applicable
on a local or regional scale where there is a dense Continuously
Operating Reference Station (CORS) network.
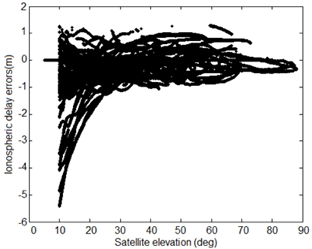
Fig. 2 Single-differenced ionospheric delay errors on GPS L1 at MOBS IGS
station. The errors were calculated from using the vertical TEC values
from the post-processed GIMs on 13 August 2014.
A Hybrid System of PPP and Network-RTK?
The notion of PPP-RTK was first described by Wübenna et al. (2005).
PPP-RTK is a synthesis of the positive characteristics of PPP and
network-RTK (Wübbena et al. 2005). Network-RTK solutions can be
generalized in two ways, i.e., the mostly commonly used technique is the
use of Observation Space Representation (OSR-RTK) such as the Virtual
Reference Station (VRS) and Flächenkorrekturparameter (FKP) techniques;
and the other is State Space Representation (SSR-RTK), or loosely termed
PPP-RTK (Collins et al. 2012).
The original concept of PPP was a precise positioning technique that
works solely on SSR corrections determined from a sparse global network
of CORS stations. Instead of lumping all error components together as
one error (i.e. correction), as is the case of OSR-RTK, SSR errors are
bettered modelled and transmitted individually. This leads to improved
performance as bandwidth can be optimized based on the spatial and
temporal characteristics of the errors. However, as it has been already
mentioned, PPP engineered in the traditional sense may never reach the
level of performance of RTK, with its possibility of instantaneous
ambiguity fixing. So, if PPP is scaled down requiring local/regional
atmospheric corrections to be provided, then the unique characteristic
of PPP as a global wide-area precise positioning technique is
compromised. Similarly, if SSR-RTK is expanded to a global scale, it is
essentially equivalent to PPP (Collins et al. 2012).
Although it may appear that PPP and RTK are not mutually exclusive, the
utility of these two techniques could be merged. This is the irony of
PPP-RTK technique. PPP is a unique positioning technique that can truly
offer global solutions without the requirements of local/regional
reference networks; whereas RTK/network-RTK will continue to dominate
regional positioning especially when a dense local/regional GNSS
infrastructure has already been established. Integration of these two
techniques would lead to improved position accuracy and convergence time
but the performance is now dependent on the extent and density of the
reference networks, which is critical for the provision of accurate
atmospheric information to aid rapid ambiguity fixing. Hence SSR-RTK is
a preferred expression as it makes a clearer distinction between the
standard PPP and RTK techniques.
Future Prospect of PPP in the context of Multi-GNSS
With the advent of modernized and other upcoming GNSS and RNSS systems,
it would be remiss of the authors not to discuss the potential benefits
of these additional constellations on the accuracy and convergence time
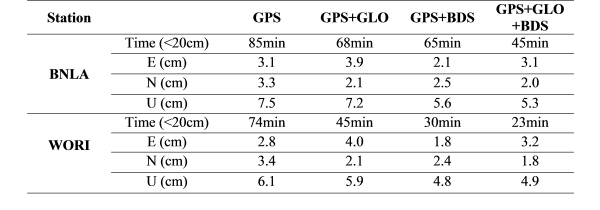
for PPP. Figure 3 shows results of multi-GNSS float-PPP solutions at two
GNSS reference stations located in Melbourne, Australia on 11 January
2015. GPS, GLONASS and BeiDou measurements were post-processed in
kinematic PPP mode. Table 2 shows the RMS errors (one-sigma) for the
East, North and Up components computed from seven days of GNSS data,
9-15 January 2015. The convergence criterion for the kinematic PPP is
that the positioning errors reach, and remain within ±20 cm. It can be
seen that the GPS+GLONASS+BeiDou PPP significantly improves the PPP
performance compared to the GPS-only solution with an average accuracy
improvements of 20% and 30% in the horizontal and vertical components,
respectively. The convergence time is shortened by about 20% when
compared to a single-constellation PPP solution (Ren et al. 2015). It is
also important to note that the time series of the multi-GNSS PPP
solutions are much more stable than the GPS-only solutions, with much
smaller and fewer fluctuations. Li et al. (2015), Chen et al. (2015) and
Tegedor et al. (2014) reported similar findings. That is, that the
addition of BeiDou, Galileo and GLONASS systems to the standard GPS-only
scenario could significantly shorten the convergence time for PPP and
improve the positioning accuracy, especially in GNSS-challenged
environments (Chen et al. 2015; Li et al. 2015; Tegedor et al. 2014).
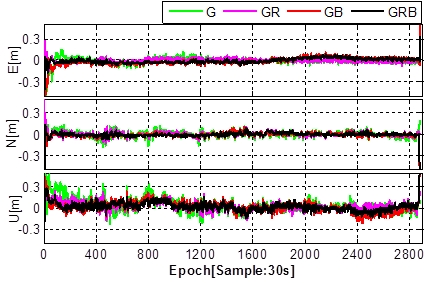
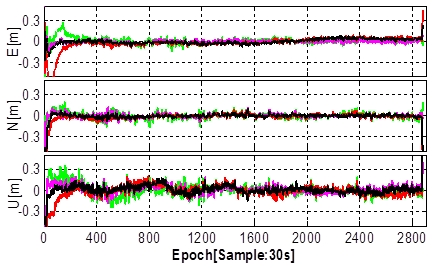
Fig. 3 Kinematic PPP processing using multi-GNSS data, i.e., GPS-only
(G), GPS+GLONASS (GR), GPS+BeiDou (GB), GPS+GLONASS+BeiDou (GRB), for
GNSS station BNLA (top) and WORI (bottom) in Melbourne, Australia on 11
January 2015 (Ren et al. 2015). These results are float-PPP solutions.
Table 2 RMS errors and convergence time of the multi-GNSS PPP kinematic
solutions based. The RMS values were computed at one-sigma using seven
days of GNSS data from 9-15 January 2015.
Furthermore, performing PPP with triple-frequency observations is now
possible with the availability of the L5 signal being transmitted by the
modernized GPS Block IIF satellites along with new satellite
constellations such as Galileo, BeiDou and QZSS (Geng and Bock 2013;
Lauricheese 2015; Tegedor and Ovstedal 2013). Triple-frequency
processing has a significant impact on ambiguity convergence time,
achieving ambiguity-fixed solutions within a few minutes or even
shorter. The accuracy of triple-frequency PPP is also subsequently
improved to about the 10 cm level within a very short period of time due
to extra-widelane ambiguity resolution, which can be completed almost
instantaneously (Lauricheese 2015). Nevertheless, issues such as
interoperability and compatibility need to be addressed to allow for
successful integration of observations from multiple constellation GNSS
systems and signals.
ENABLING REAL-TIME PPP
In this section, we will look at the two types of critical
infrastructure that are necessary for implementing real-time PPP: (a)
availability of precise satellite orbit and clock correction products in
real-time; and (b) dissemination of corrections allowing users to
operate with comparative ease.
Availability of Precise Satellite Orbits and Clocks
The IGS has been providing precise satellite orbit and clock corrections
for more than a decade and these products are freely available over the
Internet. The IGS orbits and clocks come in various forms and are
delivered with some delay, to support post-processed applications. For
example, the IGS Final satellite orbit and clock products are of the
highest accuracy but are delivered with a latency of 12–18 days. Through
its Real-Time Service (RTS), the IGS extends its capability to support
PNT applications requiring real-time access to the IGS products and GNSS
data streams. At present, the IGS-RTS provides GPS corrections as
official products. The GLONASS products are currently provided as
experimental products and will soon be included within the service when
the RTS reaches its full operating capability. Other constellations will
be added to the portfolio products over time.
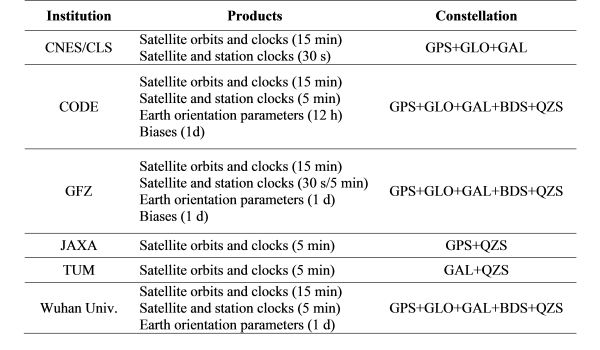
In addition, the IGS is providing multi-GNSS precise orbit and clock
products, through the IGS Multi-GNSS Experiment (MGEX) in order to gain
experience and insight into multi-GNSS processing, so as to ultimately
support multi-GNSS applications. Five MGEX analysis centers are
presently contributing multi-GNSS products in various combinations and
sampling rates as show in Table 3 (Montenbruck et al. 2014). The MGEX
analysis centers are the Centre National d'Etudes Spatiales (CNES),
Center for Orbit Determination in Europe (CODE), GeoForschungsZentrum
Potsdam (GFZ), Japan Aerospace Exploration Agency (JAXA), Technische
Universität München (TUM). Since 2015, CNES and JAXA real-time analysis
centres are also generating real-time correction streams enabling
multi-GNSS PPP.
Table 3: An overview of the available IGS MGEX products as of October
2015.
Correction Dissemination Methods
Another requirement for real-time PPP is the communication channel(s)
used to disseminate the correction data. These correction data need to
be transmitted via a communication link to users in a standard format
and protocol, which would allow GNSS receiver manufacturers to implement
them in their receivers’ firmware. The correction dissemination methods
can be grouped into terrestrial-based using the Internet or cellular
delivery method; and space-based transmission using satellites.
Currently, the corrections enabling real-time PPP, i.e., the IGS RTS,
are freely available via the Internet. These corrections are streamed in
the RTCM (Radio Technical Commission for Maritime Services) SSR format.
The NTRIP (Networked Transport of RTCM via Internet Protocol) stream
transport protocol is used to disseminate the correction data. Some
commercial service providers such as Trimble and Fugro are also
providing real-time PPP service in propriety formats, via terrestrial
communication links and L-band communication satellites.
Space-based systems are the ideal communications link for SSR correction
data transmission, as it does not suffer from the ground-based
telecommunication issues of connectivity, latency, standards and
transmission on different radio frequencies. Furthermore, the
space-based delivery method is more in line with the view that PPP is a
global wide-area positioning technique. Ideally, the dissemination of
SSR correction data is preferred with a GNSS-compatible signal, to avoid
the need for additional communications hardware at the user end to
access the SSR corrections. Galileo and QZSS (Quasi-Zenith Satellite
System) have augmentation signals capable of transmitting these
corrections.
The L6 signal (formerly known as the “LEX signal”) being transmitted by
the QZSS is an example of a space-based delivery channel that enables
real-time PPP. When fully deployed in 2023, QZSS will consist of four
satellites in highly inclined elliptical orbits and three geostationary
satellites. The goal of QZSS is to enhance the availability and
performance of GNSS over Japan and the region centered on the 135°E
meridian. In addition to the navigation signals that are interoperable
with GPS, QZSS also transmits two augmentation signals, i.e. L1S
(formerly known as “L1-SAIF”) and L6. The L1S is compatible with the
aviation-style SBAS (Satellite-Based Augmentation System), which
provides submeter-level accuracy wide-area differential corrections, as
well as integrity for safety-of-life services. The L6 signal, on the
other hand, is designed to enable high accuracy real-time positioning.
A joint research project between the Australian Cooperative Research
Centre for Spatial Information (CRCSI) and JAXA established between
2013-2015 aimed at evaluating the feasibility of utilizing the QZSS L6
signal to deliver high accuracy real-time precise positioning for
Australian PNT users (Choy et al. 2015). The transmission of regional or
national messages for precise positioning is of interest for Australia
as its ground telecommunication network required for the implementation
of the network-RTK technique is limited and mainly concentrated in urban
areas. Transmission of GNSS corrections via a satellite-link allows
large areas to be serviced. Figure 4 shows the performance of static GPS
PPP solutions for the RMIT GNSS reference station in real-time on 1
August 2013, using the L6 signal with precise GPS satellite orbits and
clocks generated by JAXA. Figure 5 shows the accuracy of real-time
kinematic GPS PPP using the L6 signal. Additional information on this
project can be found in Choy et al. (2015). Table 4 outlines the RMS
values of the real-time kinematic PPP solutions, i.e., GPS-only and
GPS+GLONASS+QZSS, using the QZSS L6 signal. The results were based on
series of real-time GNSS data collected at a GNSS reference station in
November 2014 and May 2015 and the data processed in kinematic PPP mode.
Note that QZSS began transmission of satellite corrections for GLONASS
and QZSS in 2014. From 2018, QZSS will transmit on the L6 signal
centimeter-level “augmentation data” generated by Mitsubishi Electric
Corporation and GEO++ to support SSR-RTK. This service will enable
instantaneous centimeter-level positioning accuracy in real-time for the
Japanese coverage area.
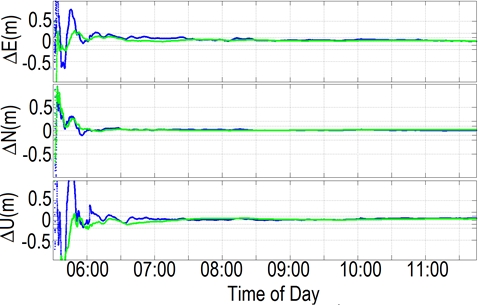
Fig. 4 Real-time PPP errors in static mode using the QZSS L6 (blue) and
the IGS (CLK-11, green) corrections. The data was collected on 1 August
2013 at the RMIT GNSS reference station located in Melbourne, Australia
(Choy et al. 2015).
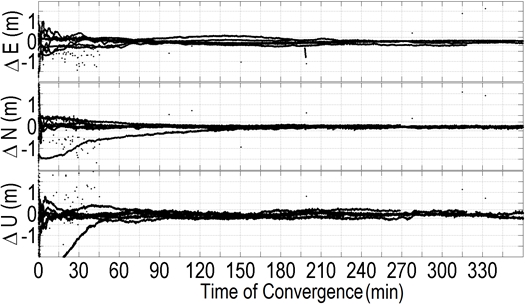
Fig. 5 Real-time PPP errors in kinematic mode using the QZSS L6
corrections. The results were based on data collected from 17-22
September 2013 at the RMIT GNSS reference station located in Melbourne,
Australia (Choy et al. 2015).
Table 4 RMS errors of the real-time kinematic PPP solutions using the
QZSS L6 signal. Series of static GNSS data were collected at the RMIT
GNSS reference station in November 2014 and May 2015 and the data were
processed in kinematic PPP mode.

CONCLUDING REMARKS
PPP is an elegant positioning technique that conforms to the original
intention of GPS usage, which is “single receiver positioning”. PPP can
in principle provide positioning solutions at centimeter-level accuracy
anywhere in the world, without the need of having one or more nearby
reference stations. PPP only requires a small number of reference
stations distributed globally, which makes this mode of positioning
highly attractive from the point of view of costs and operationally
complexity. The PPP technique is especially useful for positioning and
navigation in remote regions where ground-based CORS infrastructure is
sparse or unavailable; as well as to cover a wide-area where investment
in the establishment and operation of a dense CORS infrastructure cannot
be justified. Although PPP presents definite advantages, its
applicability is currently limited by the long convergence time, of the
order of tens of minutes, even with implementation of ambiguity
resolution procedures and multi-GNSS observation processing.
The key to instantaneous convergence for PPP is the availability of
accurate ionospheric delay corrections. The requirements on accuracy for
these corrections are very challenging, which currently mandates a dense
well-distributed CORS infrastructure similar to that of network-RTK. The
attractiveness of PPP lies in the state-space representation of errors,
which provides a high level of flexibility and scalability.
Fundamentally in regions where CORS infrastructure exists, RTK-like
performance could be expected. With improved modeling of ionospheric
delay error, the separation of CORS can be extended, from tens to
hundreds of kilometers. Fixed-PPP solutions would then be possible at
all times and all locations. However, if this system is expanded to a
global scale without a dense CORS network, then the performance would
fundamentally be equivalent to that of PPP.
PPP has come a long way, and is capable of delivering high accuracy
point positioning solutions in post-processing mode, and more recently
in real-time, as demonstrated both in commercial services and by
academic researchers. Nonetheless PPP still requires further algorithm
development to reduce the convergence time, e.g., triple-frequency PPP;
as well as to provide quality indicators, along with accurate PPP
solutions to gain industry acceptance for real-time use, especially for
safety- and liability-critical applications. What is also interesting
now is we are seeing a shift in technological and infrastructure design
so as to broadcast PPP corrections as an inherent value-added service by
GNSS satellites, e.g. in the case of QZSS and Galileo, and perhaps also
for BeiDou. This evolution would be significant as it would enhance the
performance of traditional single receiver GNSS positioning, and would
bring immense benefits to our society.
To conclude, PPP and RTK were originally developed independently of each
other in order to support different purposes. It is expected that these
two modes of positioning will likely co-exist for many years to come.
RTK will continue to deliver GNSS users with high accuracy instantaneous
positioning, while PPP will complement RTK by providing the flexibility,
scalability and efficiency to meet the demand of future PNT
applications.
Acknowledgments
The authors wish to acknowledge the efforts of all the entities
contributing to the IGS for providing products for PPP; Ken Harima from
RMIT University and Paul Collins from Natural Resources Canada (NRCan)
who provided some of the figures and results presented herein;
colleagues who provided insight, data and stimulating discussions that
greatly assisted in the preparation of this paper. The authors
gratefully acknowledge the anonymous reviewers for carefully reading the
paper and providing constructive comments. This paper was produced as
part of the work of the International Association of Geodesy (IAG)
Working Group 4.5.2: Precise Point Positioning and Network RTK and the
International Federation of Surveyors (FIG) Working Group 5.4: GNSS.
References
Banville S, Langley R (2009) Improving real-time kinematic PPP with
instantaenous cycle-slip correction. Proc. ION GNSS 2009, Institute of
Navigation, Savannah, USA. 22-25 September, 2470-2478
Bertiger W, Desai S, Haines B, Harvey N, Moore A, Owen S, Weiss J (2010)
Single Receiver Phase Ambiguity Resolution with GPS Data. Journal of
Geodesy 84(5):327-337
Bisnath S, Collins P (2012) Recent Developments in Precise Point
Positioning. GEOMATICA 66(2):375-385
Bisnath S, Gao Y (2009) Current State of Precise Point Positioning and
Future Prospects and Limitations. Observing Our Changing Earth,
International Association of Geodesy Symposia, Springer-Verlag, Berlin,
Heidelberg 133: 615-623
Chen J et al. (2015) A simplified and unified model of multi-GNSS
precise point positioning. Advances in Space Research 55(1): 125–134
Choy S, Harima K, Li Y, Choudhury M, Rizos C, Wakabayashi Y, Kogure S
(2015) GPS Precise Point Positioning with the Japanese Quasi-Zenith
Satellite System LEX Augmentation Corrections. Journal of Navigation
68(4):769–783
Collins P (2008) Isolating and Estimating Undifferenced GPS Integer
Ambiguities. Proc. ION NTM 2008, Institute of Navigation, San Diego,
California, USA. 28-30 January, 720-732
Collins P, Bisnath S (2011) Issues in Ambiguity Resolution for Precise
Point Positioning. Proc. ION GNSS 2011, Institute of Navigation,
Portland, Oregon, USA. 19-23 September, 679-687
Collins P, Henton J, Mireault Y, Heroux P, Schmidt M, Dragert H, Bisnath
S (2009) Precise Point Positioning for Real-Time Determination of
Co-Seismic Crustal Motion. Proc. ION GNSS 2009, Institute of Navigation,
Savannah, USA. 22-25 September, 2479-2488
Collins P, Lahaye F, Bisnath S (2012) External Ionospheric Constraints
for Improved PPP-AR Initialisation and a Generalised Local Augmentation
Concept. Proc. ION GNSS 2012, Institute of Navigation, Tennessee, USA.
17-21 September, 3055-3065
Colombo O, Sutter A, Evans A (2004) Evaluation of Precise, Kinematic GPS
Point Positioning. Proc. ION GNSS 2004, Institute of Navigation, Long
Beach, California, USA. 21-24 September, 1423-1430
Gao Y, Shen X (2002) A New Method for Carrier-Phase-Based Precise Point
Positioning. Navigation 49(2):109-116
Ge M, Gendt G, Rothacher M, Shi C, Liu J (2007) Resolution of GPS
Carrier-Phase Ambiguities in Precise Point Positioning (PPP) with Daily
Observations. Journal of Geodesy 82(7):389-399.
doi:10.1007/s00190-007-0208-3
Geng J (2010) Rapid Integer Ambiguity Resolution in GPS Precise Point
Positioning. Ph.D., The University of Nottingham
Geng J, Bock Y (2013) Triple-frequency GPS precise point positioning
with rapid ambiguity resolution. Journal of Geodesy 87(5):449-460
Geng J, Meng X, Dodson A, Teferle F (2010) Integer Ambiguity Resolution
in Precise Point Positioning: Method Comparison. Journal of Geodesy
84(9):569-581. doi:10.1007/s00190-010-0399-x
Hèroux P et al. (2004) Products and Applications for Precise Point
Positioning - Moving Towards Real-Time. Proc. ION GNSS 2004 Meeting,
Institute of Navigation, Long Beach, California, USA. 21-24 September,
1832-1843
Hèroux P, Kouba J (2001) GPS Precise Point Positioning Using IGS Orbit
Products. Physics and Chemistry of the Earth Part A 26(6-8):573-578
Juan JM et al. (2012) Enhanced Precise Point Positioning for GNSS Users.
IEEE T Geosci Remote 50(10):4213-4222. doi:10.1109/Tgrs.2012.2189888
Kouba J (2009) A Guide to using International GNSS Service (IGS)
Products. http://igscb.jpl.nasa.gov/components/usage.html.
Lauricheese D (2015) Handling the Biases for Improved Triple-Frequency
PPP Convergence. GPS World. April 2015.
Laurichesse D, Mercier F, Bertias J, Broca P, Cerri L (2009) Integer
Ambiguity Resolution on Undifferenced GPS Phase Measurements and its
Applications to PPP and Satellite Precise Orbit Determination
Navigation. Navigation 56(2):135-149.
Li X, Zhang X, Ge M (2010) Regional reference network augmented precise
point positioning for instantaneous ambiguity resolution. Journal of
Geodesy 85(3):151-158
Li X, Zhang X, Ren X, Fritsche M, Wickert J, Schuh H (2015) Precise
positioning with current multi-constellation Global Navigation Satellite
Systems: GPS, GLONASS, Galileo and BeiDou. Sci Rep-Uk 5 doi:ARTN
832810.1038/srep08328
Montenbruck O, Steigenberger P, Khachikyan R, Weber G, Langley R,
Mervart L, Hugentobler U (2014) IGS-MGEX: Preparing the Ground for
Multi-Constellation GNSS Science. Inside GNSS, January/February 2014.
Ren X, Choy S, Harima K, Zhang X (2015) Multi-Constellation GNSS Precise
Point Positioning using GPS, GLONASS and BeiDou in Australia. In: IGNSS
Symposium Gold Coast, Australia, 14-16 July, paper 52
Rizos C, Janssen V, Roberts C, Grinter T (2012) Precise Point
Positioning: Is the Era of Differential GNSS Positioning Drawing to an
End? Paper presented at the FIG Working Week 2012, Rome, Italy, 6-10
May, paper 5909
Seepersad G, Bisnath S (2013) Integrity monitoring in Precise Point
Positioning. Proc. ION GNSS 2013, Institute of Navigation, Nashville,
Tennessee, USA. 16-20 September
Seepersad G, Bisnath S (2014) Challenges in Assessing PPP Performance.
Journal of Applied Geodesy 8(3):205-222
Shi J (2012) Precise Point Positioning Integer Ambiguity Resolution with
Decoupled Clocks. Ph.D., University of Calgary
Tegedor J, Ovstedal O (2013) Triple Carrier Precise Point Positioning
(PPP) Using GPS L5. Survey Review 46(337):288-297.
doi:10.1179/1752270613Y.0000000076
Tegedor J, Ovstedal O, Vigen E (2014) Precise orbit determination and
point positioning using GPS, GLONASS, Galileo and BeiDou. Journal of
Geodetic Science 4(1):2081-9943
Teunissen P (1997) On the GPS widelane and its decorrelating property.
Journal of Geodesy 71(9):577-587
Teunissen P, Khodabandeh A (2015) Review and principles of PPP-RTK
methods. Journal of Geodesy 89(3):217-240 doi:10.1007/s00190-014-0771-3
Witchayangkoon B (2000) Elements of GPS Precise Point Positioning.
Ph.D., The University of Maine, USA
Wübbena G, Schmitz M, Andreas B (2005) PPP-RTK: Precise Point
Positioning Using State-Space Representation in RTK Networks. Proc. ION
GNSS 2005, Institute of Navigation, Long Beach, California, USA. 13-16
September, 2584-2594
Zhang X, Li X (2012) Instantaneous re-initialization in real-time
kinematic PPP with cycle slip fixing. GPS Solution 16(3):315-327
Zumberge J, Heflin M, Jefferson D, Watkins M, Webb F (1997) Precise
Point Positioning for The Efficient and Robust Analysis of GPS Data From
Large Networks. Journal of Geophysical Research 102(B3):5005-5017
Zumberge J, Webb F, Bar-Sever Y (2001) Precise Post Processing of GPS
Data Products and Services from JPL. Proc. ION NTM 2001, Institute of
Navigation, Long Beach, CA, 22-24 January, 250-253
Author Biographies
Suelynn Choy is senior lecturer of Surveying and Geodesy at RMIT
University, Melbourne Australia. Her research interests are in the areas
of GNSS precise positioning and atmospheric remote sensing. Suelynn is
currently the co-chair of the IAG Working Group 4.4.2 on Integer
Ambiguity Resolution for Multi-GNSS PPP and PPP-RTK" and FIG Working
Group 5.4 on GNSS.
Sunil Bisnath is an Associate Professor of Geomatics Engineering in
the Department of Earth and Space Science and Engineering at the
Lassonde School of Engineering at York University in Toronto, Canada.
His research interests over the past two decades focus on precise GNSS
positioning and navigation for a multitude of applications. He
holds an Honours B.Sc. and M.Sc. in Surveying Science from the
University of Toronto and a Ph.D. in Geodesy and Geomatics Engineering
from the University of New Brunswick.
Chris Rizos is Professor of Geodesy and Navigation at the
University of New South Wales, Sydney, Australia. Chris is the immediate
past president of the International Association of Geodesy (IAG) and
co-chair of the Multi-GNSS Asia Steering Committee. Chris is a Fellow of
the IAG, a Fellow and current president of the Australian Institute of
Navigation, and a Fellow of the U.S. Institute of Navigation.

